Trigonometry:

Below is a rough guide to trigonometry mostly borrowed from Wikipedia. Probably the easiest way to learn trig is through some of the excellent online instructional videos out there, which take you through all the material in baby steps. Below is a video from YouTube user KhanAcademy If you'd like an excellent series of instructional videos in mathematics, I highly recommend checking out this guy's videos and website.

For more educational resources be sure to visit http://www.khanacademy.org/

Overview

In this right triangle: sin A = a/c; cos A = b/c; tan A = a/b.

If one angle of a triangle is 90 degrees and one of the other angles is known, the third is thereby fixed, because the three angles of any triangle add up to 180 degrees. The two acute angles therefore add up to 90 degrees: they are complementary angles. The shape of a right triangle is completely determined, up to similarity, by the angles. This means that once one of the other angles is known, the ratios of the various sides are always the same regardless of the overall size of the triangle. These ratios are given by the following trigonometric functions of the known angle A, where a, b and c refer to the lengths of the sides in the accompanying figure:

The sine function (sin), defined as the ratio of the side opposite the angle to the hypotenuse.

$\sin A=\frac{\textrm{opposite}}{\textrm{hypotenuse}}=\frac{a}{\,c\,}\,.$

The cosine function (cos), defined as the ratio of the adjacent leg to the hypotenuse.

$\cos A=\frac{\textrm{adjacent}}{\textrm{hypotenuse}}=\frac{b}{\,c\,}\,.$

The tangent function (tan), defined as the ratio of the opposite leg to the adjacent leg.

$\tan A=\frac{\textrm{opposite}}{\textrm{adjacent}}=\frac{a}{\,b\,}=\frac{\sin A}{\cos A}\,.$

The hypotenuse is the side opposite to the 90 degree angle in a right triangle; it is the longest side of the triangle, and one of the two sides adjacent to angle A. The adjacent leg is the other side that is adjacent to angle A. The opposite side is the side that is opposite to angle A. The terms perpendicular and base are sometimes used for the opposite and adjacent sides respectively. Many people find it easy to remember what sides of the right triangle are equal to sine, cosine, or tangent, by memorizing the word SOH-CAH-TOA (see below under Mnemonics).

The reciprocals of these functions are named the cosecant (csc or cosec), secant (sec) and cotangent (cot), respectively. The inverse functions are called the arcsine, arccosine, and arctangent, respectively. There are arithmetic relations between these functions, which are known as trigonometric identities.

With these functions one can answer virtually all questions about arbitrary triangles by using the law of sines and the law of cosines. These laws can be used to compute the remaining angles and sides of any triangle as soon as two sides and their included angle or two angles and a side or three sides are known. These laws are useful in all branches of geometry, since every polygon may be described as a finite combination of triangles.

Graphing process of y = sin(x) using a unit circle.

Graphing process of y = tan(x) using a unit circle.

Graphing process of y = csc(x) using a unit circle.

Extending the definitions

Graphs of the functions sin(x) and cos(x), where the angle x is measured in radians.

The above definitions apply to angles between 0 and 90 degrees (0 and p/2 radians) only. Using the unit circle, one can extend them to all positive and negative arguments (see trigonometric function). The trigonometric functions are periodic, with a period of 360 degrees or 2p radians. That means their values repeat at those intervals. The tangent and cotangent functions also have a shorter period, of 180 degrees or p radians.

The trigonometric functions can be defined in other ways besides the geometrical definitions above, using tools from calculus and infinite series. With these definitions the trigonometric functions can be defined for complex numbers. The complex exponential function is particularly useful.

e x + i y = e x (cos y + i sin y).

See Euler's and De Moivre's formulas.

Mnemonics

A common use of mnemonics is to remember facts and relationships in trigonometry. For example, the sine, cosine, and tangent ratios in a right triangle can be remembered by representing them as strings of letters, as in *SOH-CAH-TOA:

Sine = Opposite ÷ Hypotenuse

Cosine = Adjacent ÷ Hypotenuse

Tangent = Opposite ÷ Adjacent

"TOA CAH SOH" -- pronounced as 'tua' 'ca' (i.e. the word 'car' without the 'r') 'so' -- means "Big Foot Lady" in Chinese dialect, which could help in remembering the ratios.

Also used is its reverse, OHSAHCOAT (pronounced oh-sah-coat). It is interpreted as OHS-AHC-OAT, as shown below.

Opposite ÷ Hypotenuse = Sine

Adjacent ÷ Hypotenuse = Cosine

Opposite ÷ Adjacent = Tangent

One way to remember the letters is to sound them out phonetically (i.e. "SOHCAHTOA").^[13] Another method is to expand the letters into a phrase, such as "Some Old Horses Chew Apples Happily Throughout Old Age".^[14]

Calculating trigonometric functions

Main article: Generating trigonometric tables

Trigonometric functions were among the earliest uses for mathematical tables. Such tables were incorporated into mathematics textbooks and students were taught to look up values and how to interpolate between the values listed to get higher accuracy. Slide rules had special scales for trigonometric functions.

Today scientific calculators have buttons for calculating the main trigonometric functions (sin, cos, tan and sometimes cis) and their inverses. Most allow a choice of angle measurement methods: degrees, radians and, sometimes, grad. Most computer programming languages provide function libraries that include the trigonometric functions. The floating point unit hardware incorporated into the microprocessor chips used in most personal computers have built-in instructions for calculating trigonometric functions.

Applications of trigonometry

Sextants are used to measure the angle of the sun or stars with respect to the horizon. Using trigonometry and a marine chronometer, the position of the ship can be determined from such measurements.

Main article: Uses of trigonometry

There are an enormous number of uses of trigonometry and trigonometric functions. For instance, the technique of triangulation is used in astronomy to measure the distance to nearby stars, in geography to measure distances between landmarks, and in satellite navigation systems. The sine and cosine functions are fundamental to the theory of periodic functions such as those that describe sound and light waves.

Fields that use trigonometry or trigonometric functions include astronomy (especially for locating apparent positions of celestial objects, in which spherical trigonometry is essential) and hence navigation (on the oceans, in aircraft, and in space), music theory, acoustics, optics, analysis of financial markets, electronics, probability theory, statistics, biology, medical imaging (CAT scans and ultrasound), pharmacy, chemistry, number theory (and hence cryptology), seismology, meteorology, oceanography, many physical sciences, land surveying and geodesy, architecture, phonetics, economics, electrical engineering, mechanical engineering, civil engineering, computer graphics, cartography, crystallography and game development.

Standard Identities

Identities are those equations that hold true for any value.

1.: $s i n 2 A + c o s 2 A = 1$

2.: $s e c 2 A - t a n 2 A = 1$

3.: $c o s e c 2 A - c o t 2 A = 1$

Angle Transformation Formulas

1.: $s i n (A + B) = s i n A * c o s B + c o s A * s i n B$

2.: $c o s (A + B) = c o s A * c o s B - s i n A * s i n B$

3.: $s i n (A - B) = s i n A * c o s B - c o s A * s i n B$

4.: $c o s (A - B) = c o s A * c o s B + s i n A * s i n B$

Common formulas

Triangle with sides a,b,c and respectively opposite angles A,B,C

Certain equations involving trigonometric functions are true for all angles and are known as trigonometric identities. Some identities equate an expression to a different expression involving the same angles. These are listed in List of trigonometric identities. Triangle identities that relate the sides and angles of a given triangle are listed below.

In the following identities, A, B and C are the angles of a triangle and a, b and c are the lengths of sides of the triangle opposite the respective angles.

Law of sines

The law of sines (also known as the "sine rule") for an arbitrary triangle states:

$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R,$

where R is the radius of the circumscribed circle of the triangle:

$R = \frac{abc}{\sqrt{(a+b+c)(a-b+c)(a+b-c)(b+c-a)}}.$

Another law involving sines can be used to calculate the area of a triangle. Given two sides and the angle between the sides, the area of the triangle is: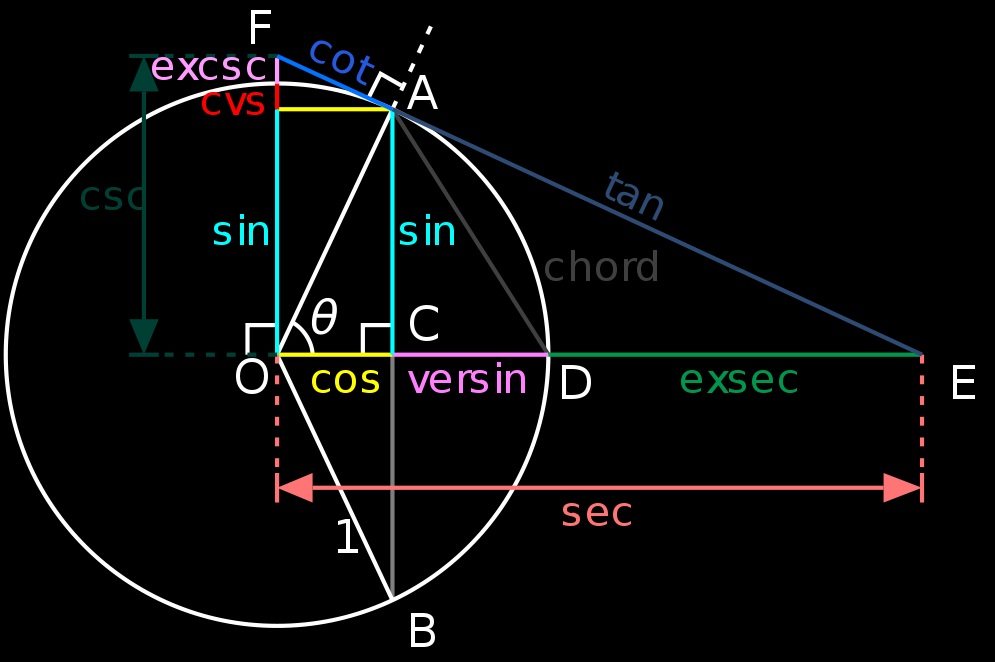

$\mbox{Area} = \frac{1}{2}a b\sin C.$

All of the trigonometric functions of an angle ? can be constructed geometrically in terms of a unit circle centered at O.

Law of cosines

The law of cosines (known as the cosine formula, or the "cos rule") is an extension of the Pythagorean theorem to arbitrary triangles:

$c^2=a^2+b^2-2ab\cos C ,\,$

or equivalently:

$\cos C=\frac{a^2+b^2-c^2}{2ab}.\,$

Law of tangents

The law of tangents:

$\frac{a-b}{a+b}=\frac{\tan\left[\tfrac{1}{2}(A-B)\right]}{\tan\left[\tfrac{1}{2}(A+B)\right]}$

Euler's formula

Euler's formula, which states that $e i x = cos x + i sin x$ , produces the following analytical identities for sine, cosine, and tangent in terms of e and the imaginary unit i:

$\sin x = \frac{e^{ix} - e^{-ix}}{2i}, \qquad \cos x = \frac{e^{ix} + e^{-ix}}{2}, \qquad \tan x = \frac{i(e^{-ix} - e^{ix})}{e^{ix} + e^{-ix}}.$